Approach: Diffusion Steering via Reinforcement Learning
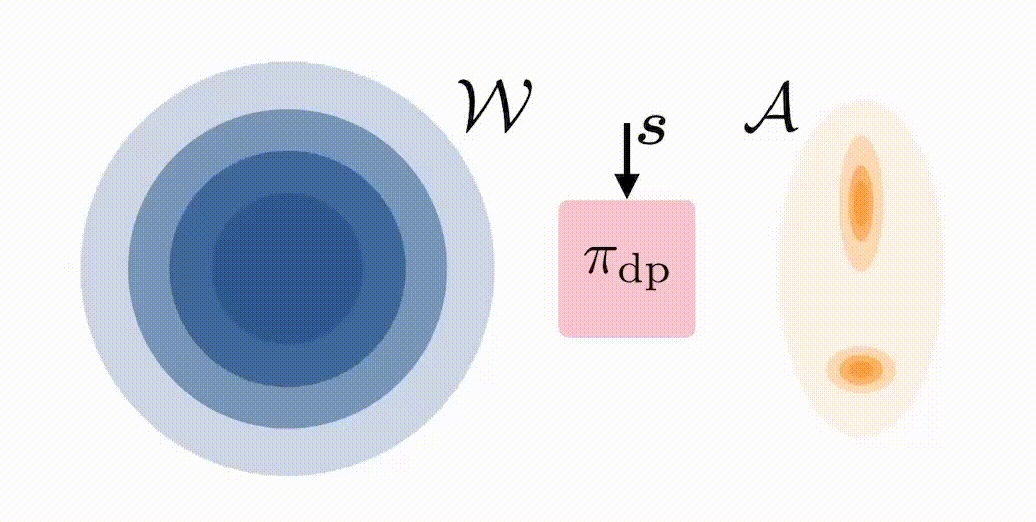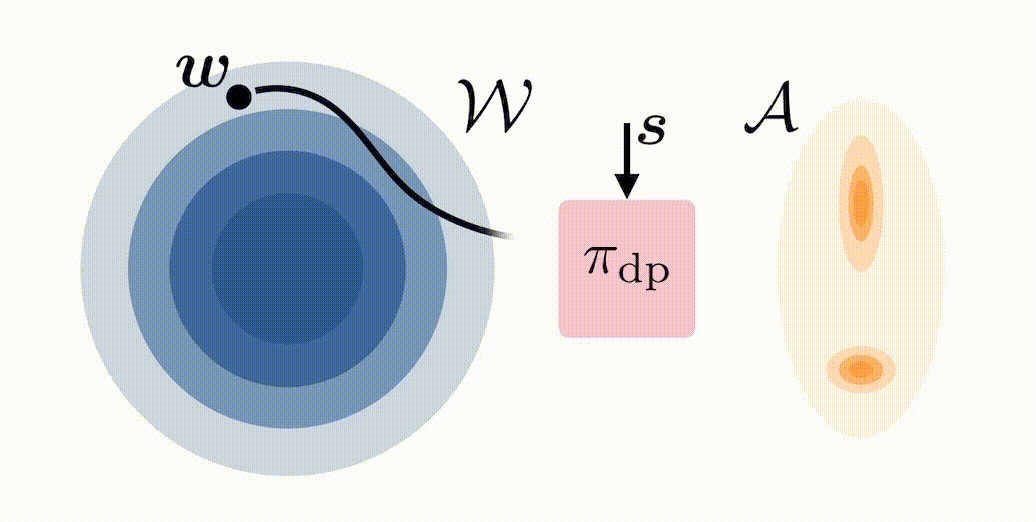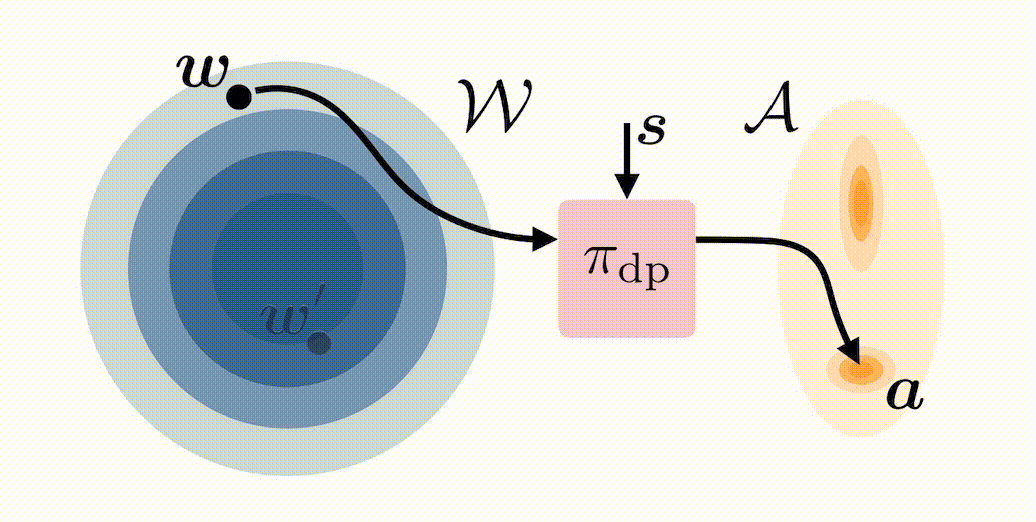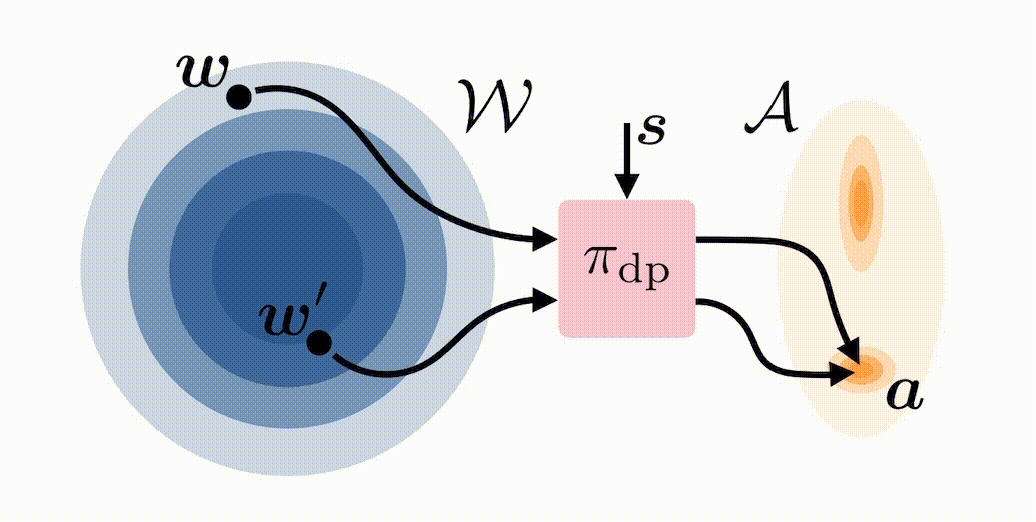
In standard deployment of a BC-trained diffusion policy \(\pi_{\mathrm{dp}}\), noise is sampled \(\boldsymbol{w} \sim \mathcal{N}(0,I)\) and then denoised through the reverse diffusion process to produce an action \(\boldsymbol{a}\). We propose modifying the initial distribution of \(\boldsymbol{w}\) with an RL-trained latent-noise space policy \(\pi^{\mathcal{W}}\) that, instead of choosing \(\boldsymbol{w} \sim \mathcal{N}(0,I)\), chooses \(\boldsymbol{w}\) to steer the distribution of actions produced by \(\pi_{\mathrm{dp}}\) in a desirable way:
We refer to our approach as DSRL: Diffusion Steering via Reinforcement Learning. Notably, DSRL:
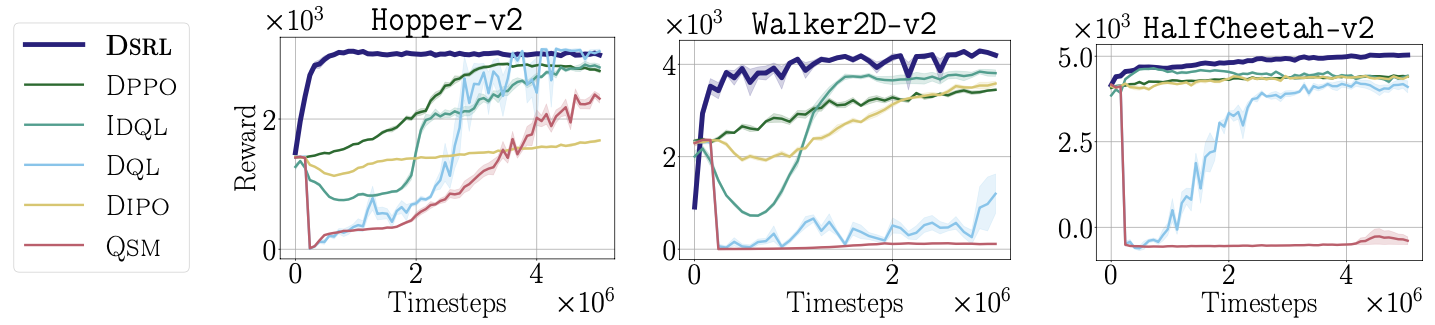
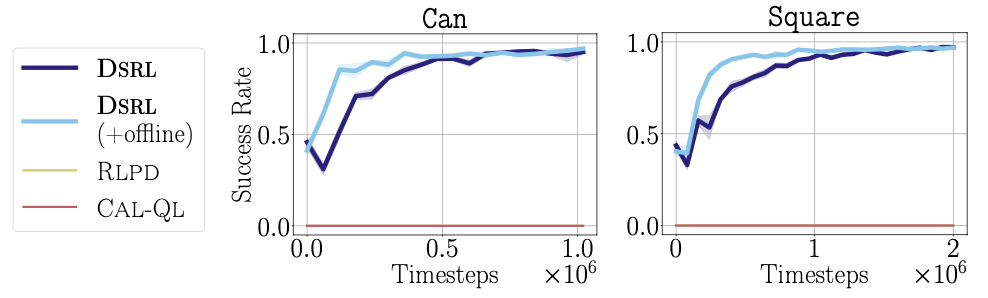
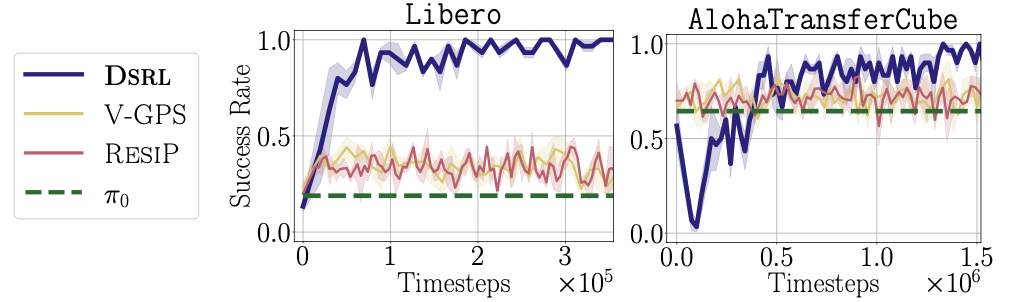
- Is highly sample efficient, enabling real-world improvement of diffusion and flow policies and achieving state-of-the-art performance on simulated benchmarks.
- Applies both to single-task diffusion policies, as well as generalist diffusion and flow policies.
- Completely avoids challenges typically associated with finetuning diffusion policies—such as back-propagation-through-time—by simply treating the noise as the action when applying RL to learn \(\pi^{\mathcal{W}}\).
- Only requires training a small MLP policy to select the noise—rather than finetuning the weights of a (potentially much larger) diffusion policy—and, indeed, does not require direct access to the weights of the base diffusion policy at all.
In the following, we provide videos demonstrating DSRL's real-world performance, and a summary of our simulated results.